DBA terrain and camp sizes
Terrain sizes
Confused by terrain sizes?
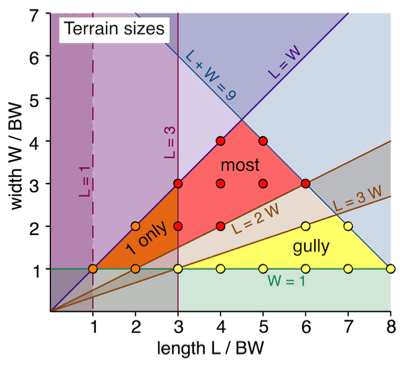
The DBA rules about terrain sizes are a little convoluted, so I thought a diagram might be useful. It is a plot of feature width (in base widths) against feature length (also in base widths).
All dimensions are in base widths (BW) unless stated otherwise.
But please read "An important note about rectangles and diagonals" at the bottom of the page!
The coloured regions
The key coloured regions are:
The lines
The lines represent the limits, based on the conditions in the rules:
The dots
These represent the integer valued solutions. So, for example, a typical terrain feature (non-gully) will be in the red region. The red dots indicate the possible sizes that are integral numbers of BW wide and long. In this case, these are: 6 x 3, 5 x 4, 5 x 3, 4 x 4, 4 x 3, 4 x 2, 3 x 3, and 3 x 2.
Some extreme values
The DBA rules about terrain sizes are a little convoluted, so I thought a diagram might be useful. It is a plot of feature width (in base widths) against feature length (also in base widths).
All dimensions are in base widths (BW) unless stated otherwise.
But please read "An important note about rectangles and diagonals" at the bottom of the page!
The coloured regions
The key coloured regions are:
- Red: all but one (at most) terrain features must be in this region.
- Orange: only one feature can be in this region
- Yellow: this regions shows the permissible sizes of gullies.
The lines
The lines represent the limits, based on the conditions in the rules:
- L + W = 9: each must fit in a rectangle of which the length plus the width is less than or equal to 9 BW.
- L = 3: only one feature can have a length less than 3 BW.
- L = 1, W = 1: every feature must have both length and width of at leas t 1 BW.
- L = 3 W: a gully's length must be at least three times its width.
- L = 2 W: the length of non-gullies must not exceed twice their width
- L = W: length is greater than or equal to width
The dots
These represent the integer valued solutions. So, for example, a typical terrain feature (non-gully) will be in the red region. The red dots indicate the possible sizes that are integral numbers of BW wide and long. In this case, these are: 6 x 3, 5 x 4, 5 x 3, 4 x 4, 4 x 3, 4 x 2, 3 x 3, and 3 x 2.
Some extreme values
- Gullies
- Longest you can have is 8 x 1.
- Widest is 6.75 x 2.25 (it is also the largest area gully).
- Smallest is 3 x 1.
- Non-gullies
- The longest is 6 x 3.
- The shortest is 1 x 1.
- The largest area is 4.5 x 4.5.
- The smallest area is 1 x 1 (for one piece of terrain only) and 3 x 1.5 (for the other pieces).
Camp sizes
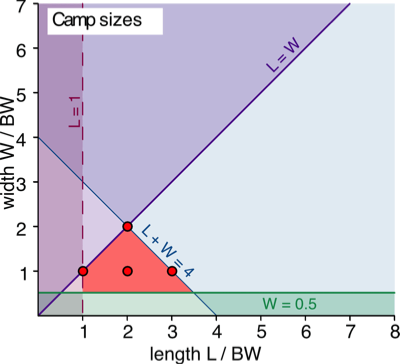
Here is a corresponding image for camp sizes.
The coloured regions
The key coloured regions is:
The lines
The lines represent the limits, based on the conditions in the rules:
The dots
These represent the integer valued solutions. 1 x 1, 2 x 1, 2 x 2, 3 x 1.
Some extreme values
The coloured regions
The key coloured regions is:
- Red: camp dimensions must be in this region.
The lines
The lines represent the limits, based on the conditions in the rules:
- L + W = 4
- L = 1: must be at least 1 BW long
- W = 0.5: must be at least 0.5 BW wide.
- L = W: length is greater than or equal to width
The dots
These represent the integer valued solutions. 1 x 1, 2 x 1, 2 x 2, 3 x 1.
Some extreme values
- Smallest area: 1 x 0.5
- Largest area: 2 x 2
- Longest: 3.5 x 0.5
- Shortest: 1 x 0.5
- Widest: 2 x 2
An important note about rectangles and diagonals
DBA states that area-features "must fit into a rectangle of which the length plus the width totals no more than 9 BW."
The largest area area-feature you can therefore have is a 4.5 BW by 4.5 BW square.
What is the smallest area-feature you can have?
You would have thought a square feature that is 1 BW x 1 BW.
However this is incorrect!. Length is defined as "maximum dimension" and width as "maximum dimension at a right angle to its length".
So the smallest feature has diagonals of 1 BW. It is therefore a square whose sides are 1/SQRT(2) BW. If 1 BW = 40 mm this equates to 28.3 mm.
The largest area area-feature you can therefore have is a 4.5 BW by 4.5 BW square.
What is the smallest area-feature you can have?
You would have thought a square feature that is 1 BW x 1 BW.
However this is incorrect!. Length is defined as "maximum dimension" and width as "maximum dimension at a right angle to its length".
So the smallest feature has diagonals of 1 BW. It is therefore a square whose sides are 1/SQRT(2) BW. If 1 BW = 40 mm this equates to 28.3 mm.